Pengertian Relasi dalam Teori Bahasa dan Automata

Relasi adalah suatu aturan yang memasangkan anggota himpunan satu ke himpunan lain. Suatu relasi dari himpunan A ke himpunan B adalah pemasangan atau perkawanan atau korespondensi dari anggota – anggota himpunan A ke anggota – anggota himpunan B.

Contoh:

Graph

Graph G2 (Bukan Graph Sederhana)

V = {1,2,3,4 }

E = {(1,2),(1,3),(2,3),(2,4),(3,4),(4,4)}

Graph G3 (Graph Berarah)

V = {1,2,3,4 }

E = {(1,2),(1,3),(2,4),(3,4)}

Penerapan Graph pada rangkaian listrik

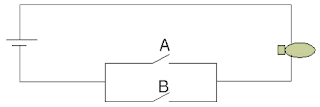
Rangkain Saklar Paralel

Saklar A	Saklar B	Lampu
On	On	On
On	Off	On
Off	On	On
Off	Off	Off

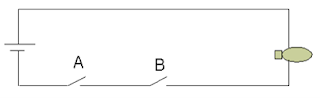
Rangkaian Saklar Seri

Saklar A	Saklar B	Lampu
On	On	On
On	Off	Off
Off	On	Off
Off	Off	Off

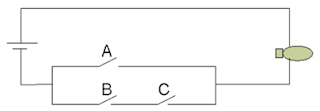
Rangkain Saklar Kombinatorial

Saklar A	Saklar B	Saklar C	Lampu
On	On	On	On
On	On	Off	On
On	Off	On	On
On	Off	Off	On
Off	On	On	On
Off	On	Off	Off
Off	Off	On	Off
Off	Off	Off	Off

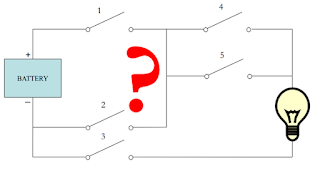
Latihan Soal Saklar

Sebutkan saklar mana saja yang mesti on/off agar lampu bisa menyala?

Jawaban:

Saklar yang harus on adalah saklar 1, 4 dan 3

Saklar yang harus off adalah saklar 2 dan 5